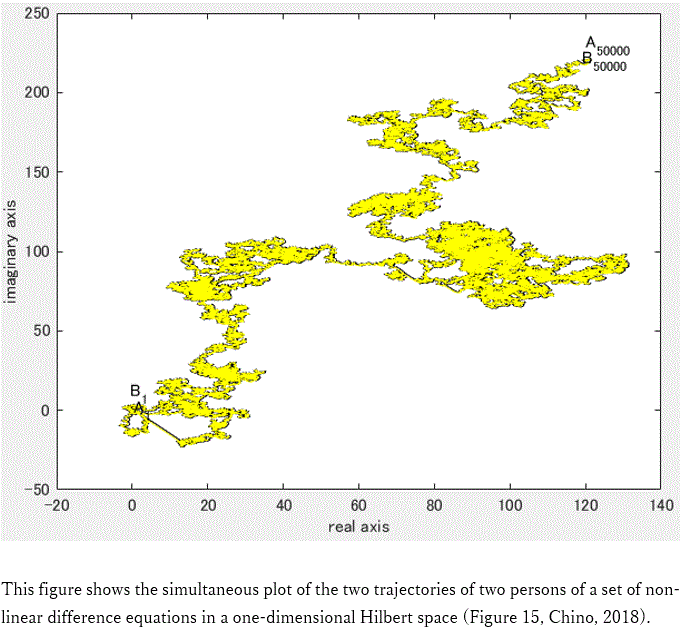
 |
 |
|
|
|
|
|

|
|
|
This page was last updated Sunday, 05-Oct-2025 12:17:00 JST. |
As discussed elesewhere (Chino, 2019a, 2020a,b,c), increasing attention has been paid to mutual interactions among
objects, especially in the medical and biological literature recently (Imai et al., 2014; Park & Greenberg, 2005;
Sato et al., 2002; Tian et al., 2016; Vega et al., 2013; Yamada et al., 2000). Interactions among objects in the
literature are generally asymmetric in contrast to those in the physical world. For example, Imai et al.
(2014) report biosynthetic pathways of nicotinamide adenine dinucleotide (NAD+). Such a pathway can be
converted into an asymmetric matrix, elements of which are binary, since it can be expressed as a certain directed
graph (digraph) in graph theory (e.g., Bang-Jensen & Guttin, 2007; Christofides, 1975). In quorum sensing, some
bacteria secrete a signaling molecule called autoinducer to their host environment and detect their number, and if
it reaches a threshold they respond again to the environment by secreting some special substance (e.g., Parsek &
Greenberg, 2005; Vega et al., 2013). Tian et al. (2016) studies the midbrain dopamine system, in which dopamine
neurons in the ventral tegmental area (VTA) are thought to compute reward prediction error (RPE) (e.g., Schultz et
al., 1997). They demonstrate that even simple arithmetic computations such as RPE are not localized in specific
brain areas but, rather, are distributed across multiple nodes in a global brain network. Such a network might
also be described by a complicated digraph whose corresponding weight matrix is generally asymmetric.
Asymmetry can be observed in the other literature such as in the social and behavioral sciences (e.g., Chino,
2012). Close (2000) summarizes various asymmetric phenomena in the various disciplines of science and discusses
the meaning of asymmetry. Chino (2020a) analyzes the trade imbalance data between 4 nations using HFM which was
proposed by Chino and Shiraiwa (1993). Chino (1978) analyzes a similar trade data between 10 nations and depicts
their asymmetric relations graphically using one of the asymmetric multidimensional scaling (asymmetric MDS) methods
in psychometrics developed by the author. Asymmetry can be analyzed using hypothesized asymmetric matrices in some
literature. For example, Sato et al. (2002) assume a hypothetical asymmetric matrix in investigating the problem of
learning to play the game of rock-paper-scissors based on the theory of games and the notion of evolutionally stable
strategy ESS introduced by Maynard and Price (1973).
In response to such a great deal of attention, Chino Institute for the Studies of
Asymmetry and Chaos (abbreviated as Chino ISAC) was established in 2020. Our mission is twofold. One is to develop
mathematical theories and statistical methods for the analysis of
asymmetric data which are observed ubiquitously as asymmetric similarity matrices (abbreviated as ASMs) among
objects in the various disciplines of sciences varying from the social and behavioral sciences to natural sciences.
For example, one-sided love and hate among members of any informal group constitute such an ASM in psychology.
Amount of migration from one region to another gives rise to ASMs in geography. Trade imbalance forms another
example. We may observe various pathways among voxels of neurons, biosynthetic pathways of nicotinamide adenine
dinucleotide in research laboratories (e.g., Imai & Guarente,2014). Sometimes, ASMs are not observed but
hypothesized. For example, payoff matrices hypothesized in the game of rock-paper-scissors are examples of ASM's
(e.g., Sato et al., 2002).
In developing these theories and methods, it will be appropriate and natural in general
to distinguish between the holistic structure and the dynamics among objects, although in the
relativity theory it is known that the gravity exerted on stars determines their space-time structure (Einstein, A.,
1916). One of the promising theories and methods for the analysis of the former might be to utilize the asymmetric
multidimensional scaling (abbreviated as asymmetric MDS) developed in psychometrics (e.g., Chino, 2012; Cox & Cox,
2001; Saburi & Chino, 2008), especially the Hermitian Form Model (abbreviated as HFM) by Chino and Shiraiwa (1993).
According to the Chino-Shiraiwa theorem proved in that paper, objects can be embedded in a finite-dimensional Hilbert
space under a mild condition. As regards the manual of HFM, see, for example, Chino (2020b). As for the relation
between the Hilbert space in HFM and that in quantum mechanics, see Chino (2020c). As regards the analysis of the
latter, we may utilize dynamical system theories developed in mathematics, especially complex dynamical system
theories (e.g., Alexander, 1994; Milner, 2000; Ueda et al., 1995).
The other mission is to apply our theories and methods to various ASM's, and is to show their effectiveness.
We shall attach MATLAB codes for these methods.
Dr. (Educational Psychology)
Emeritus Professor of Aichi Gakuin University
chino@dpc.agu.ac.jp
Mar 1970 BA in Educational Psycholgy, Nagoya University
Mar 1972 MA in Educational Psychology, Nagoya University
Nov 1994 PhD in Educational Psycholgy, Nagoya University
Please send questions and comments to
chino@dpc.aichi-gakuin.ac.jp
![]()
Recent research interests
![]()
Recent publications
![]()
Recent research reports
![]()
Books and lectures
Book
-Springer-book.jpg)
![]()
Recent conference papers & invited lectures
Chino, N. (2014b).
A general non-Newtonian n-body problem and dynamical scenarios of solutions.
Handout presented at the 42th annual meeting of The Behaviormetric
Society of Japan, September 3, Sendai, Japan. (partly in Japanese)
![]()