このページは、令和2年4月24日に一部更新しました。
![]()
| 1.3.6.1 プログラムとその概要 |
| 1.3.6.2 プログラムのダウンロードコーナー |
| 1.3.6.3 出力結果の概要 |
| 1.3.6.4 ミラーリエル錯視データの出力結果の概要 |
1.3.6.1 節のプログラムには、最初に長いコメントが付けてある。また、同一データ に対する anova プロシジャと glm プロシジャの両方のプログラムが併記してある。さ らに、最後に分散分析の前提についての幾つかの検討のためのプログラムも載せてあ る。その結果、長いプログラムになっているので、幾つかに分けて示しながら、順に それらの概要を解説する。
1.3.6.2 節では、当該プログラムの必要個所をパソコンのフロッピー等にコ ピーし保存(ダウンロード)できるような表形式のクリック箇所を用意してある。 ユーザーは、それらの中から必要なものを選んで自分用に書き換えればよい。
1.3.6.3 節では、これらの一連のプログラムによる出力結果の説明を行う。
冒頭で述べたように、プログラムはつぎの表にまとめたように幾つかに分けて示しな がら、順にそれらの概要を解説する:
*-------------------------------------------------------------------------* | November 23, 1995 | | sas program -- cr4kirk.anova | | | | Example of a CR-p ANOVA design analysis for Kirk (1982) Table 4.3.1 | | data (p.140). This data has 4 levels with 32 subjects, i.e., CR-4 | | ANOVA design. | | | | Cautions: | | | | (1) According to Winer (1971), Bartlett's test for homogeneity of vari- | | ance (Bartlett, 1937) is the most widely used test. However, the rou- | | tine use of it as a preliminary test is not recommended. For, it is | | extremely sensitive to nonnormality (Scheffe, 1959, p.83). | | (2) Test for homogeneity of variance may be unnecessary for balanced | | designs like this data set. | | (3) Proc anova must be used only for balanced designs. | | (4) For pairwise comparisons, the tukey procedure is superior to the | | Scheffe procedure. | | (5) Use cldiff option in the mean statement for all pairwise compari- | | sons. | | (6) CLDIFF is the default for unbalanced designs unless DUNCAN, REGWF, | | REGWQ, SNK, or WALLer is specified. | | (7) Lsmeans option is not available with proc anova. | | (8) Proc glm can be used for balanced or unbalanced designs. | | (9) Contrast statement is not available with proc anova. | | (a) Proc anova has outstat option and outputs ss, df, f-values etc. | | (b) Proc glm has not only the outstat option but also output statement | | which computes various indices for glm, such as residuals of the | | model. | | | *-------------------------------------------------------------------------*; |
この項では、完全無作為化デザイン(独立測度1要因デザイン)及びそのデータを SAS で分析する場合の注意事項を列記した。この項は、SAS のコメント文の1つを 用いて書いてあるので、実際のプログラムにはこの項は削除しても何ら影響はない。
options ps=60 ls=80;
/* (1) data input */
data work;
do level=1 to 4;
input y @;
output;
end;
label level='sleep deprivation, 12, 24, 36, 48h'
y='magnitude of hand steadiness';
cards;
3 4 7 7
6 5 8 8
3 4 7 9
3 3 6 8
1 2 5 10
2 3 6 10
2 4 5 9
2 3 6 11
;
|
上述のプログラムの概要は、つぎの通りである。まず、(1) の data input では、 プログラム中でデータを定義し input 文で必要な変数名 level 及び y を付けている。 ここで、要因の4つの水準のコードは、cards 文の下のデータの中にはなく、do 文 を用い level という名の変数の添字をデータを読み込みながら定義していることに 注意せよ。もちろん、水準のコードをあらかじめデータとして用意しておくことも 可能である。また、input 文の変数 y の後にある $@$ 記号にも注意せよ。これは、 SAS では「行保持 at 記号」(trailing at sign) と呼ばれ、この例のように input 文で定義されている変数は1つしかないにも拘わらず、データの読み込み開始位置を つぎの行に移さず(この例では4つ分のデータを読み終わるまで)保持する。
/* (2-1) CR-4 ANOVA using proc anova */ title 'CR-4 ANOVA for the Kirk (1982, p.140) data'; proc anova data=work; class level; model y=level; means level/tukey alpha=0.01; /* means level/tukey cldiff alpha=0.01; */ run; |
(2-1) の項では、完全無作為化デザインデータを anova プロシジャを使って 実行するためのものである。class 文で要因名を指定し、model 文で等号の左辺に 分散分析すべき従属変数名(この例では、y)を、右辺に要因名を指定する。means 文では、この例のように要因名の後にスラッシュをつけ多重比較の方法(この例では Tukey 法)を指定する。alpha= は、多重比較の有意水準を指示するためのものであ る。means 文の後になにも指定せずセミコロンのみを付けておくと、多重比較は 行わず各水準の平均値等の情報のみを出力する。cldiff オプションは、Tukey 法や Scheff\'e 法などで総当たり方式、すなわちすべての平均値間の対比較を行い、 かつ平均値の差の区間推定も出力させたいときに指定する。これを指定しないと、 通常の方式で平均値を大きい順に並べ多重比較を行うのみとなる。ただし、非釣り 合い型デザインでは、cldiff はデフォルトになっている。
/* (2-2) Means plot using proc means output */ title 'means of each level of the factor'; proc means data=work; var y; class level; output out=temporal mean=aver; run; options ps=30 ls=80; proc plot data=temporal; plot aver*level; run; |
(2-2) の項では、means プロシジャを用いて各水準の従属変数の平均値を計算させ、 それを一時ファイルに掃き出し、plot 文を使ってそれを図に描くためのものである。 このやり方は、あまりスマートな方法ではない。より簡単な方法は、(3-2) に示した means プロシジャを用いず (3-1) の glm プロシジャにより lsmeans 文を用い out= オプションで一旦一時ファイルに掃き出し、掃き出された変数 lsmean を使い平均値 をプロットするものである。
/* (3-1) CR-4 ANOVA using proc glm */ options ps=60 ls=80; title 'CR-4 ANOVA by proc glm'; proc glm data=work; class level; model y=level; means level; means level/tukey alpha=0.01; /* means level/tukey cldiff alpha=0.01; */ lsmeans level/ out=glmout; run; |
(3-1) の項では、anova でなく glm プロシジャを用いて (2-1) と同様な分析を するためのプログラムを示した。このデータのように釣り合い型デザインでは、anova でもよいが、非釣り合い型の場合 glm を用いる必要がある。
/* (3-2) means plot using proc glm/lsmeans output option */ options ps=30 ls=80; title 'means plot utilizing proc glm/lsmeans'; proc plot data=glmout; plot lsmean*level; run; |
(3.2) の項では、既に説明したように means プロシジャを用いず (3-1) の glm プロシジャを用いて完全無作為化法のプログラムを実行した時に付随的に得られる lsmeans 文による各水準の平均値 lsmean を用いて plot 文により平均値のプロット を行わせる。
/* (4) non-pairwise contrasts using proc glm/contrast statement */ options ps=60 ls=80; title 'pairwise and non-pairwise contrasts'; proc glm data=work outstat=glmstat; class level; model y=level; means level/tukey alpha=0.01; contrast 'level 1 vs the other' level 3 -1 -1 -1; contrast 'level 1-2 vs level 3-4' level 1 1 -1 -1; contrast 'level 1-2-3 vs level 4' level 1 1 1 -3; output out=temp residual=resid; run; data work2; set glmstat; if _type_ ne 'CONTRAST' then delete; i=4; n=32; ndf=i-1; ddf=n-i; fschef=f/ndf; pschef=1-probf(fschef,ndf,ddf); drop ndf ddf i n; run; title 'sas original and scheffe adjusted F tests'; proc print data=work2; run; |
(2-1) や (3-1) の方法での多重比較は対比較に限定されるが、(4) での contrast
文を用いれば非対比較が可能となる。ただし、この方法では means 文で Tukey や
scheffe オプションを指定する場合と異なり、多重比較に際して族あたりの危険率
はコントロールされないことに注意が必要である。これを行うには、glm プロシジャの
オプション, outstat= のところで例にあるように、各対比の F-値等を一時ファイル
(この例では glmstat)に掃き出しておいて、つぎの data 文に示したように、掃
き出し結果を使って
Scheff\'e 法
により危険率のコントロールを行ってやればよい。
最後に、ここでの glm プロシジャの最後の output 文は後続の (5-1) での誤差項の
度数分布の作成や (5-2) の項での誤差項の正規性検定のために、誤差項の推定値を
一時ファイル temp に変数名 resid を付けて保存させるためのものである。
(4) での最後の print プロシジャは、直前の data 文で計算されたScheff\'e 法に より修正された対比検定の F-値をプリントさせるためのものである。
/* (5-1) posterior analysis (1): histogram plot of error estimates */ options ps=30 ls=80; title 'histogram of the error estimates '; proc chart data=temp; vbar resid; run; |
(5-1) の項は、既に説明済みであるので省略する。
/* (5-2) posterior analysis (2): test for normality of error estimates */ options ps=60 ls=80; title 'test for global normality of the dependent variable'; proc univariate data=temp normal; var resid; run; |
(5-2) の項は、既に説明済みであるので省略する。
/* (5-3) posterior analysis (3) : test for homogeneity of variances */ title 'Bartlett test for homogeneity of variances'; proc discrim data=work pool=test slpool=0.05; class level; var y; run; |
(5-3) の項では、水準間の分散の等質性の検定を行うためのプログラムである。
| 以下に、前節のプログラムを各自のフロッピーやハードディスクにダウンロードする ためのファイルのリンク先を示す。各自の必要とするプログラムをクリックし、対応 する画面が現れたら、マウスによる通常の手続きで自らのパソコンのフロッピーなり ハードディスクにダウンロードするとよい。ただし、c) 以降 j) までの各プログラム については、単独では作動しないものがほとんどであるので、注意されたい。という のは、これらについては、それ以前のプログラムで定義したり掃き出したりした一時 的ファイルを使うことを前提にしているからである: |
(2-1) のプログラムによる最初の主要な結果として、つぎのような分散分析表 が出力される:
従属変数: y magnitude of hand steadiness
変動因 自由度 平方和 平均平方 F 値 Pr > F
Model 3 194.5000000 64.8333333 44.28 <.0001
Error 28 41.0000000 1.4642857
Corrected Total 31 235.5000000
R2 乗 変動係数 誤差の標準偏差 y の平均
0.825902 22.51306 1.210077 5.375000
変動因 自由度 Anova 平方和 平均平方 F 値 Pr > F
level 3 194.5000000 64.8333333 44.28 <.0001
|
うえの結果を見ると、変動因 (Source) が2種類出力されている。SAS では 分散分析結果は、どのようなモデルを指定しても最初に誤差以外の項による変動因を Model、誤差の変動分を Error とした分散分析表を出力し、以降順次 Model の 構成要因のそれぞれについての効果の検定結果を表示する。この例は、たまたま 1要因なので、Model の項とつぎに表示されるその構成要因(ここでは level)は 一致する。
(2-1) のプログラムにおけるつぎの出力結果は、means 文で指定した変動因 level の水準間の tukey 法による対比(とりわけ対比較)検定に関するものである。 means 文のパラメータで alpha=0.01 と指定しているので、すべての対比較の危険率 を全体として1パーセント水準に押さえたうえでどの対間で平均値の差が有意である のかを表示する。これを示したのが、つぎの表である。
y における Tukey のスチューデント化範囲 (HSD) 検定
NOTE: この検定は第 1 種の実験全体での過誤を制御しますが、 一般的に第 2
種の過誤は REGWQ より高いです。
アルファ 0.01
誤差の自由度 28
誤差の平均平方 1.464286
スチューデント化範囲の棄却値 4.82959
最小な有意差 2.0662
ラベルがすべての水準で同じ文字であるとき、どの対比較も統計的には有意ではありませ
ん。
Tukey グループ 平均 N level
A 9.0000 8 4
B 6.2500 8 3
C 3.5000 8 2
C
C 2.7500 8 1
|
この指定を行うと、うえのように4つの水準の平均値を大きい順に並べ、さらに どこに統計的な有意差があるかを Tukey Grouping と表示した項にアルファベット をつけることにより示す。うえの結果では、平均値が最大の水準とつぎに大きい水準 間、及び2番目と3番目に大きい水準間では有意差があるが、3番目と4番目の水準 間では有意差がないことを、示している。
これに対して、もし means 文にさらに cldiff オプションを加えると、すべての 水準間の差を総当たり方式で推定し、検定結果も加える。
MEANS プロシジャ
分析変数 : y magnitude of hand steadiness
sleep
deprivation,
12, 24, オブザべーション
36, 48h 数 N 平均 標準偏差 最小値 最大値
------------------------------------------------------------------------------------------
1 8 8 2.7500000 1.4880476 1.0000000 6.0000000
2 8 8 3.5000000 0.9258201 2.0000000 5.0000000
3 8 8 6.2500000 1.0350983 5.0000000 8.0000000
4 8 8 9.0000000 1.3093073 7.0000000 11.0000000
------------------------------------------------------------------------------------------
|
さらに、うえの出力結果に続いて、つぎのような平均値のプロット結果が得られる:
プロット : AVER*LEVEL. 凡例 : A = 1 OBS, B = 2 OBS, ...
AVER |
10 +
|
| A
|
8 +
|
|
| A
6 +
|
|
|
4 +
| A
| A
|
2 +
|
---+------------------+------------------+------------------+--
1 2 3 4
sleep deprivation, 12, 24, 36, 48h
NOTE: 1 オブザベーションが欠損値です.
|
pairwise and non-pairwise contrasts 15
2010年06月13日 日曜日 午後05時06分16秒
GLM プロシジャ
従属変数: y magnitude of hand steadiness
対比 自由度 対比平方和 平均平方 F 値 Pr > F
level 1 vs the other 1 73.5000000 73.5000000 50.20 <.0001
level 1-2 vs level 3-4 1 162.0000000 162.0000000 110.63 <.0001
level 1-2-3 vs level 4 1 140.1666667 140.1666667 95.72 <.0001
|
ただし、うえの結果は既に注意を促したように、
族あたりの危険率をコントロールしていない。
実際、このデータの場合、例えば最初の対比の係数は (3, -1, -1, -1) であり、
対比の推定値の値は、1.3.2 節の (1.17) 式及びここ
での出力結果 3. での各水準の平均値を用いて、3×2.75 - 1×3.5 -1×6.25 -1×9.00
= -10.5 となる。ここで、族あたりの危険率のコントロールを行わない対比の検定
ては、1.3.3 節の (1.28) 式を用いるとすれば、
この式の右辺の分母の値のルートの中の項も必要となる。このうち、UE
の値は、ここでの出力結果の 2. anova プロシジャによる分散分析結果のところの、
誤差の平均平方の項に既にでているように、1.46428571 である。また、UE
の右側の項は
[32+(-1)2+(-1)2+(-1)2]/8 であり、
3/2 となる。これらより、(1.28) 式の t の2乗、すなわち F-値は 50.1951221 と
計算でき、うえの SAS の出力結果である 50.20 と一致する。
この結果は、SAS では独立測定要因の contrast 文による対比検定においては、
(1.28) 式で表される t-検定方式(その2乗は F となるので、F-検定)を取ってい
ることになり、各対比をいわば計画的直交対比的に
扱って検定しており、族あたりの危険率のコントロールは行っていないことを意
味する。
そこで、もしこれらの対比が非計画的(もしくは事後的)
非直交対比 であるとすれば、(4) の後半の data 文により、
Scheff\'e 法を
用いて危険率のコントロールを行うのが望ましかろう。
sas original and scheffe adjusted F tests
OBS _NAME_ _SOURCE_ _TYPE_ DF SS
1 y level 1 vs the other CONTRAST 1 73.500
2 y level 1-2 vs level 3 CONTRAST 1 162.000
3 y level 1-2-3 vs level CONTRAST 1 140.167
OBS F PROB fschef pschef
1 50.195 .000000104 16.7317 .000002015
2 110.634 3.1182E-11 36.8780 7.3374E-10
3 95.724 1.5557E-10 31.9079 .000000004
|
このデータの場合、もともと Scheff\'e 修正する前でさえ p-値はきわめて小さい ので、Scheff\'e 修正を行っても実質的には p-値(PSCHEF と表示)は変わらない とみてよいが、詳細に値を比較検討すると修正前に比べて p-値はおよそ倍ほどに なっていることがわかる。
(5-1) の項では、事後解析の1つとして、分散分析モデルの残差項が果たして 正規分布に従っているかどうかを検討するために、まず残差のヒストグラムを描かせる ために、chart プロシジャを実行させる。実行結果は、つぎのようになる;
histogram of the error estimates
Frequency
| *****
| ***** *****
10 + ***** *****
| ***** *****
| ***** *****
| ***** *****
| ***** *****
5 + ***** ***** *****
| ***** ***** *****
| ***** ***** ***** *****
| ***** ***** ***** *****
| ***** ***** ***** ***** *****
--------------------------------------------------------------------
-1.8 -0.6 0.6 1.8 3.0
RESID 中間点
test for global normality of the dependent variable
|
うえのヒストグラムが、正規分布母集団からの無作為サンプルであると言えるか どうかを検討するのが、(5-2) の項の univariate プロシジャを利用するもので、 結果はつぎのようになる:
test for global normality of the dependent variable 18
2010年06月13日 日曜日 午後05時06分16秒
UNIVARIATE プロシジャ
変数 : resid
モーメント
N 32 重み変数の合計 32
平均 0 合計 0
標準偏差 1.15003506 分散 1.32258065
歪度 0.67866436 尖度 0.78948286
無修正平方和 41 修正済平方和 41
変動係数 . 平均の標準誤差 0.2032994
基本統計量
位置 ばらつき
平均 0.00000 標準偏差 1.15004
中央値 -0.12500 分散 1.32258
最頻値 -0.75000 範囲 5.25000
四分位範囲 1.37500
NOTE: 5 個の最頻値があります (度数 : 3)。 表では最頻値のなかで最も小さな値を表示
します。
位置の検定 H0: Mu0=0
検定 --統計量--- -------p 値-------
Student の t 検定 t 0 Pr > |t| 1.0000
符号検定 M -1 Pr >= |M| 0.8555
符号付順位検定 S -15 Pr >= |S| 0.7628
正規性の検定
検定 ----統計量---- -------p 値-------
Shapiro-Wilk W 0.970689 Pr < W 0.5186
Kolmogorov-Smirnov D 0.086046 Pr > D >0.1500
Cramer-von Mises W-Sq 0.036963 Pr > W-Sq >0.2500
Anderson-Darling A-Sq 0.258016 Pr > A-Sq >0.2500
分位点 ( 定義 5 )
分位点 推定値
100% 最大値 3.250
99% 3.250
95% 2.000
90% 1.500
75% Q3 0.625
50% 中央値 -0.125
25% Q1 -0.750
10% -1.250
UNIVARIATE プロシジャ
変数 : resid
分位点 ( 定義 5 )
分位点 推定値
5% -1.750
1% -2.000
0% 最小値 -2.000
極値
----最小値---- ----最大値----
値 Obs 値 Obs
-2.00 4 1.00 24
-1.75 17 1.50 6
-1.50 18 1.75 7
-1.25 27 2.00 32
-1.25 19 3.25 5
|
うえの出力結果のうち、正規性の検定結果は中程の W:Normal の項であり、 右端の p-値からこの場合、誤差項は正規分布母集団からの無作為サンプルと言える。
最後の (5-3) の項では、やはり分散分析の前提の1つである、水準間の 分散の等質性の検定を、discrim プロシジャで行う。結果は、つぎのようになる。 前後にいろいろな付属的な結果が出力されるが、それらは無視するとよい;
Bartlett test for homogeneity of variances
DISCRIM プロシジャ
OBS 数 32 全体の自由度 31
変数の数 1 群内の自由度 28
群水準の数 4 群間の自由度 3
判別変数の水準の詳細
事前
level 変数名 度数 重み 比率 確率
1 _1 8 8.0000 0.250000 0.250000
2 _2 8 8.0000 0.250000 0.250000
3 _3 8 8.0000 0.250000 0.250000
4 _4 8 8.0000 0.250000 0.250000
群内の共分散行列の情報
共分散行列の
共分散行列の 行列式の
level ランク 自然対数
1 1 0.79493
2 1 -0.15415
3 1 0.06899
4 1 0.53900
プール 1 0.38137
DISCRIM プロシジャ
群内の共分散行列の等質性の検定
Notation: K = Number of Groups
P = Number of Variables
N = Total Number of Observations - Number of Groups
N(i) = Number of Observations in the i'th Group - 1
__ N(i)/2
|| |Within SS Matrix(i)|
V = -----------------------------------
N/2
|Pooled SS Matrix|
_ _ 2
| 1 1 | 2P + 3P - 1
RHO = 1.0 - | SUM ----- - --- | -------------
|_ N(i) N _| 6(P+1)(K-1)
DF = .5(K-1)P(P+1)
_ _
| PN/2 |
| N V |
Under the null hypothesis: -2 RHO ln | ------------------ |
| __ PN(i)/2 |
|_ || N(i) _|
is distributed approximately as Chi-Square(DF).
カイ 2 乗 自由度 Pr > ChiSq
1.821619 3 0.6102
Since the Chi-Square value is not significant at the 0.05 level, a
pooled covariance matrix will be used in the discriminant function.
Reference: Morrison, D.F. (1976) Multivariate Statistical
Methods p252.
|
うえの $\chi^2$-検定結果から、このデータの場合、水準間の分散の等質性は 確保されていると言える。
ここでは、うえの鏡映描写データと異なるもう1つの完全無作為化デザインデータ として、ミラーリ エル錯視データを取り上げる。データは、平成30年度計量心理学 演習の13名の受講者による もので、30度15mm、30度30mm、30度45㎜ 条件での錯視 条件に対し、各被験者を無作為に割り当て た。図1は、このデータに対する完全無作為化デザイン ANOVA の SAS プログラムを示す。ここでも 同プログラム中の冒頭部にデータを入れている。
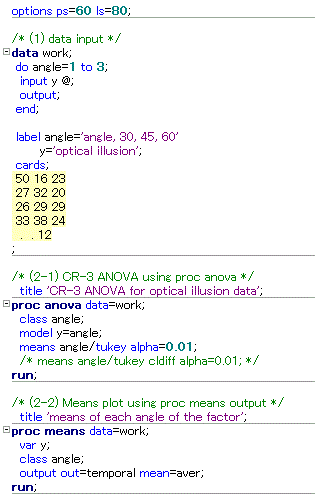
| プログラムのダウンロード・コーナー |
| cr3-illusion.sas |
うえの SAS プログラム中のデータ入力部、すなわち cards 文の下には、30度条件の4人のデータ 50, 27, 26, 33 及び最後に欠測値を示すピリオド "." が1つ、45度条件の同じく4人のデータ 16, 32, 29,38 及び最後のピリオド "." が1つ、最後の3列目は、60度条件の5人のデータ 23, 20, 29, 24, 12 が入力してあることに注意せよ。この入力書式では、データの各行に3個の データが入っていることを仮定しているので、最後の行は上記のように、5人目のデータを30度 条件と45度条件では欠測値として読み込ませる必要がある。 図2は、上記データに対する完全無作為化デザイン ANOVA による分散分析表を示す。
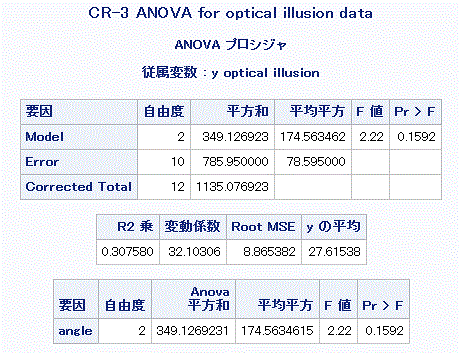
図2の F-統計量の p-値から、角度要因の効果は有意ではないことがわかる。このデータでは、相対的に は、要因の効果によるデータのばらつきに比べ、誤差によるばらつきが大きかったことを示している。図1の プログラムの中のデータを見ると、最後のデータの錯視量が12と、他のサンプルのそれに比べてかなり 小さいことが誤差のばらつきを大きくする一因である可能性がある。
図3は、同データの角度の3水準ごとのデータの平均をプロットしたものである。